Ao lançar uma moeda uma vez, qual é a probabilidade de sair cara? Pergunta fácil. Se uma moeda for honesta, é de 50%. Em outras palavras, se você apostar cara como resultado e ela se concretizar, você ganha; caso contrário, você falha. Sucesso ou não sucesso, ocorrência ou não ocorrência, ganhar uma venda ou não ganhar, todos esses resultados podem ser traduzidos como 0 e 1. A moeda é um dos casos em que você não pode controlar as probabilidades.
No entanto, no mundo real, os eventos não ocorrem aleatoriamente, sem qualquer controle dos resultados, e para nós, é apenas uma questão de identificar corretamente as variáveis que afetam essas probabilidades. A concretização de uma venda pode ser alcançada ajustando o preço do produto, melhorando a qualidade e os gastos com publicidade, etc. A rotatividade de funcionários pode ser controlada identificando os incentivos mais eficazes e evitando aqueles que, neste caso, estão positivamente correlacionados com a rotatividade de funcionários. E assim por diante.
Neste artigo, mostrarei uma técnica usada para identificar e estimar essas probabilidades: o modelo logístico. Usando este modelo, você também pode identificar as variáveis que mais impactam os resultados.
Mas antes, alguns conceitos. Se desejar, você pode pular o próximo tópico (indo diretamente para os tópicos 2 e 3).
Boa leitura!
1. Alguns conceitos
Sucesso/não sucesso é um resultado binário e segue o que chamamos de distribuição de Bernoulli com probabilidade p de ocorrer e probabilidade 1-p de não ocorrer, e a soma de p e 1-p é 1 (100%).
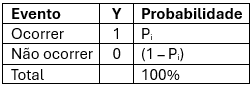
A distribuição de Bernoulli é um caso especial da distribuição binomial, onde uma única tentativa é conduzida (nesse caso n seria igual à 1 em uma distribuição binomial) e a escreveríamos como abaixo:
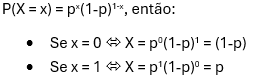
Como a resposta é uma variável binária, muitos cientistas de dados erroneamente utilizam regressão linear para estimar essas probabilidades (0 e 1).
Considere a seguinte equação linear:

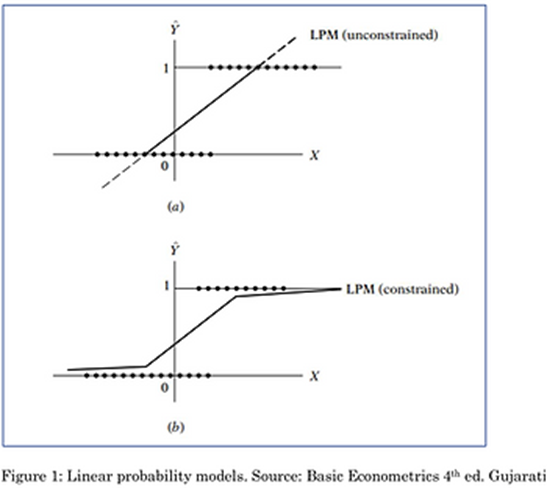
A equação acima representa o modelo de probabilidade linear (MPL) e corresponde a uma linha reta. Neste caso, ninguém pode garantir que os resultados (Pi ou Yi) respeitarão os limites [0,1]. Dependendo do valor de Xi, Ŷi pode ser negativo ou maior que 1, a menos que as seguintes restrições sejam aplicadas:
1 – se Ŷi for negativo, considere 0 como previsão.
2 – se Ŷi for maior que 1, considere 1 como previsão.
Abaixo, as
figuras que representam o MPL sem (a) e com as restrições (b):
Uma maneira melhor de garantir adequadamente que as probabilidades condicionais estimadas E(Yi) estejam entre 0 e 1 é usar modelos probit ou logit. Ambos apresentam resultados semelhantes, mas, neste artigo, mostrarei como extrair informações úteis do modelo logit (ou modelo de regressão logística). Diferentemente do modelo linear, onde a probabilidade é uma transformação linear da variável Xi (Pi = β1 + β2Xi), em um modelo de regressão logística as probabilidades de ocorrência e não ocorrência são dadas por:
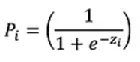
e
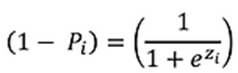
onde o termo zi = β1 + β2Xi e é chamado logit.
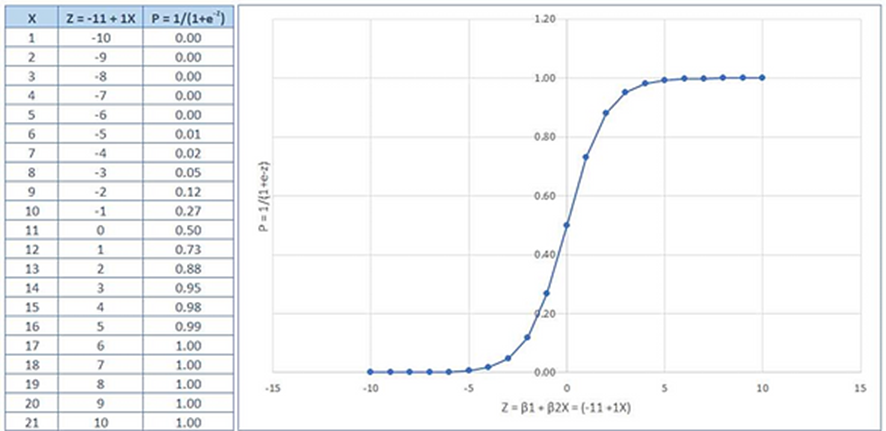
Observe na figura abaixo que o logit é uma transformação linear de X e a função de probabilidade se transforma em uma curva sigmoide de -∞ a +∞ com os limites [0,1].
Uma métrica
interessante é chamada de razão de chances: p/(1-p). Ela representa o quanto a
probabilidade de ocorrência é maior (ou menor) do que a de não ocorrência.
Assim, por exemplo, se a probabilidade de ocorrência de vendas é 0,8, a de não
ocorrência é 0,2. Nesse caso, a razão de chances é 4, indicando que a
probabilidade de ocorrência é 4x maior do que a de não ocorrência. Uma chance
de 50/50 (como a nossa moeda) tem uma razão de chances de 1. Portanto, se a
ocorrência for um bom evento (como vendas), a melhor ação é manter essa razão
acima de 1, e a probabilidade de vendas será maior do que a probabilidade de
não vendas.
Conceitualmente, o logit é calculado a partir dessa métrica como o logaritmo da razão de chances (a probabilidade de ocorrência dividida pela não ocorrência).
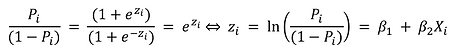
Além disso, se:
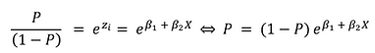
Então,
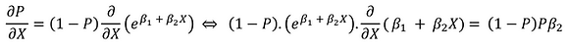
2. Por que tudo isso importa?
A análise é bastante simples. Se o logit representa o logarítmico da razão de chances, podemos descobrir o quanto a variável X impactará a ocorrência de um evento, simplesmente encontrando a exponencial dos coeficientes (lembre-se: a exponencial também é chamada de anti-logaritmo).
Para uma melhor visualização, considere o exemplo hipotético. Suponha que você tenha um grande banco de dados com consultas históricas de seus clientes, com algumas consultas em que o cliente confirmou o pedido de venda (1) e algumas consultas em que o cliente não confirmou (0). Nessa situação, metade dos clientes comprou seus produtos e a outra metade não, então sua razão de chances atual é 1 (50%/50%).
Você sabe que não está competindo em um mercado com produtos homogêneos (quando os clientes não percebem diferenças entre seus produtos e os produtos de seus concorrentes), então, neste caso, você deve identificar no banco de dados as variáveis relevantes que levariam os clientes a fechar os pedidos, além do preço do produto. Como seus produtos possuem algum grau de diferenciação, variáveis como durabilidade do produto, garantia, preço, capacidade e velocidade do produto (supondo um laptop) e muitas outras "qualidades" percebidas pelos clientes devem ser adicionadas ao modelo. Você fez isso e, após executar uma regressão logística, encontrou a seguinte equação:
Vendas (sim ou não) = -25,93 + 0,3(garantia) + 0,5(durabilidade) - 0,10(preço)
Para resumir esta exemplificação, vamos supor que as outras variáveis não foram estatisticamente significativas, apenas estas 3. A garantia é medida em meses, a durabilidade em anos e o preço em 000/R$.
Pergunta: O que os coeficientes indicam sobre a probabilidade de vendas?
Garantia: o coeficiente é 0,3, portanto, mantendo todos os outros preditores constantes, a probabilidade de um cliente confirmar o pedido aumenta em 0,3*(0,5*0,5) = 7,5% a cada mês adicionado na garantia.
A probabilidade que era de 50% aumentará para 57,5%, e a razão de chances aumentará 35% (0,575/0,425 = 1,35). Esse aumento na razão de chances é confirmado pela exponenciação do coeficiente:
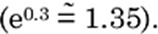
Durabilidade: o coeficiente é 0,5, portanto,
mantendo todos os outros preditores constantes, a probabilidade de um cliente
confirmar o pedido aumenta em 0,5*(0,5*0,5) = 12,5% a cada ano adicionado à
durabilidade. A probabilidade anterior aumentará de 50% para 62,5%, e a razão
de chances aumentará 66% (0,625/0,375 = 1,66). Esse aumento na razão de chances
é confirmado pela exponenciação do coeficiente:
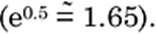
Preço: neste caso, o coeficiente é negativo (-0,10), portanto, mantendo todos os outros preditores constantes, a probabilidade de um cliente confirmar o pedido diminui em -0,1*(0,5*0,5) = -2,5% para mil dólares adicionados ao preço do produto. A probabilidade anterior diminuirá de 50% para 47,5%, e a razão de chances diminuirá 10% (0,475/0,525 = 0,90). Essa diminuição na razão de chances é confirmada pela exponenciação do coeficiente:
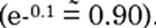
Observe que esta é uma análise feita com números hipotéticos, apenas para contextualizar o quão poderosa é a regressão logística. Em nosso exemplo, a melhoria na qualidade pode causar um aumento de preço e os resultados em vendas seriam um percentual líquido considerando os aumentos na durabilidade e no preço.
Outro ponto: a melhoria na durabilidade também pode comprometer sua própria demanda (produtos duram mais), então, em vez de um bom resultado, você pode ter o oposto (uma redução no número de pedidos feitos por seus clientes).
3. Outros exemplos de aplicação do modelo
Existem muitos outros exemplos do uso desta técnica, aqui estão alguns:
• Análise de risco de crédito com base na renda do cliente, inadimplências anteriores, valor da dívida atual, etc.
• Perda de funcionários com base na satisfação no trabalho, renda mensal, horas extras, distância da residência, etc.
• Aprovação do cliente com base nas características do produto, como por exemplo, qualidade do vinho com base nas características físico-químicas (Wine Quality - UCI Machine Learning Repository). Neste caso, a variável de resposta varia de 1 a 10, portanto, não é binomial.
Alguém pode considerar um valor menor que 7 como de gosto ruim e um valor maior ou igual a 7 como de gosto bom.
Outra opção é usar a regressão logística multinomial.
Mas isso é assunto para outro artigo…